Sierpinski

The Sierpinski Triangle is a fractal named after a Polish mathematician named Wacław Sierpinski, who is best known for his work in an area of math called set theory. Here’s how it works. We start with an equilateral triangle, which is one where all three sides are the same length:

Now we repeat the following rule on this triangle indefinitely:

The Rule: Whenever you see an equilateral triangle, like the one below on the left, chop it up into four little equilateral triangles, and get rid of the middle upside-down triangle, so you’re left with the thing on the right.

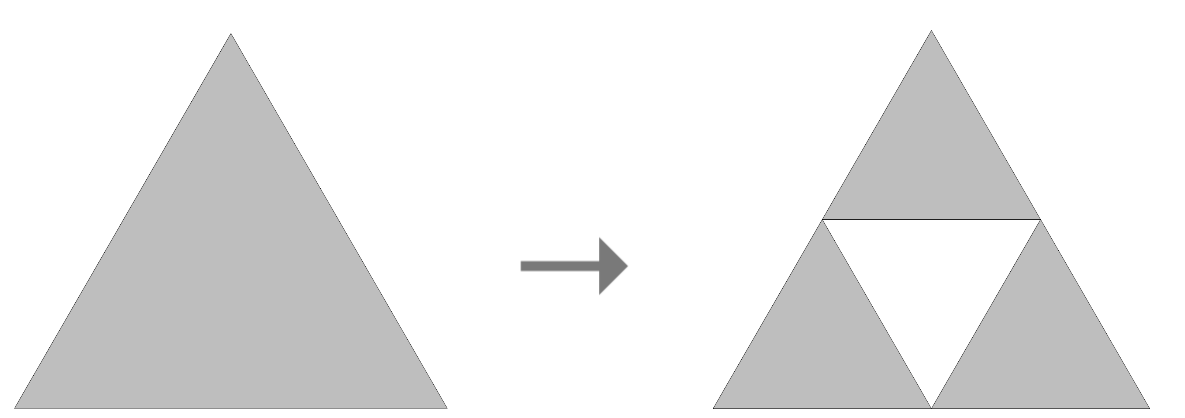
Now let’s try it for our beginning triangle. First, we apply The Rule once:

Now for each of those little gray triangles we have left, we’ll apply The Rule again:

And we’re left with more little gray triangles, so we can apply The Rule again:

And we’ll always keep getting smaller and smaller gray triangles, so we can keep doing this for as long as we want, even off to infinity:

 

 

 

There we have it. That’s the Sierpinski Triangle.

To get to know the Sierpinski Triangle better, here’s some food for thought:

• When we applied The Rule for the first time, we started with one triangle and ended up with three. How many little triangles do we have after applying The Rule 2 times? 3 times? 20 times? $n$ times?
• We keep chopping little pieces out of the triangle every time we apply The Rule. If we keep doing this forever, what’s left? In other words, what’s the area of the Sierpinski Triangle?

Now, Sierpinski didn’t stop at the triangle. He extended this concept of chopping up and taking away, and he applied it to a square. Here’s the Rule: Whenever you see a square, break it into nine smaller squares and remove the middle one.

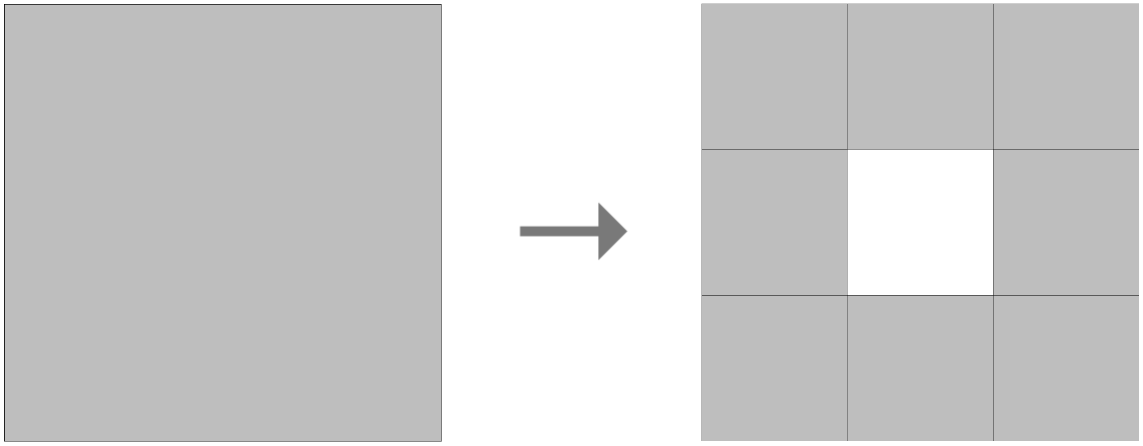
You’re left with eight smaller squares, so you can apply the Rule again to each one.

And, again, we can keep doing this as long as we want.

 

 

This is called the Sierpinski Carpet.

But that’s not all you can do with this concept! You can also take it into three dimensions. Take, for instance, a tetrahedron:

We can chop this tetrahedron up so we have three little tetrahedra and a gap in the middle.

Image by Robert Dickau

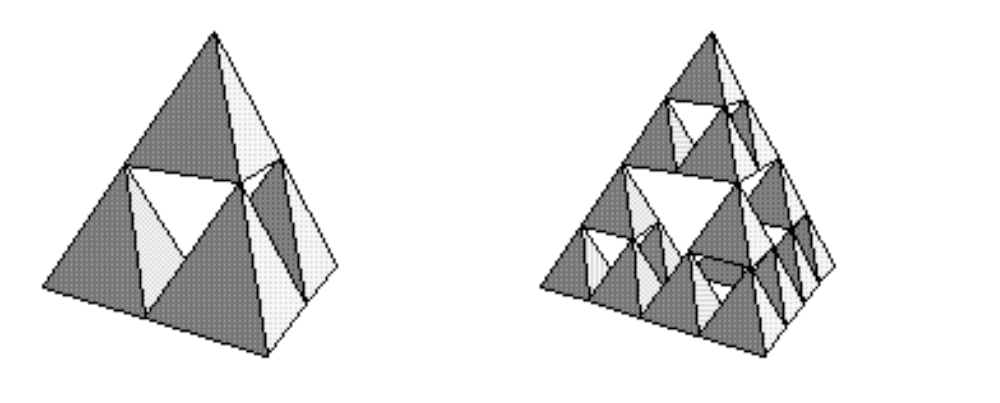
This is a really cool variation to try to build yourself! Here’s an interesting question to think about: When we chop out the middle of the tetrahedron, what’s the shape of the piece we’re getting rid of? (Hint: This time, it’s not just another little tetrahedron!)

What if we tried extending the Sierpinski Carpet into three dimensions, too, so we’re chopping up a cube? What might that look like? Take a guess, and then look up the Menger sponge. (Yes, Menger… not Sierpinski. On the matter of shape-chopping, a mathematician named Karl Menger picked up where Sierpinski left off.)

How else might you extend Sierpinski’s chopping-up concept?