Pascal's Triangle

In the beginning, there was an infinitely long row of zeroes. And somewhere in the midst of these zeroes there was a lonely 1.

To this long row was applied a certain rule:

The figure then looked like this.

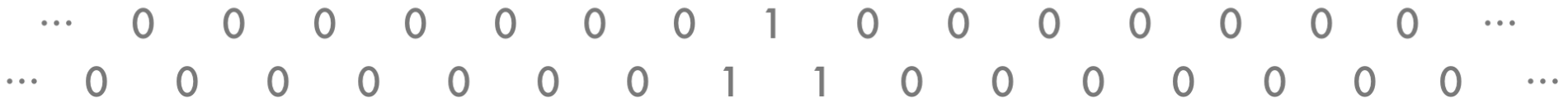
That wasn’t exciting enough, so the rule was applied to the new row that had just been generated.

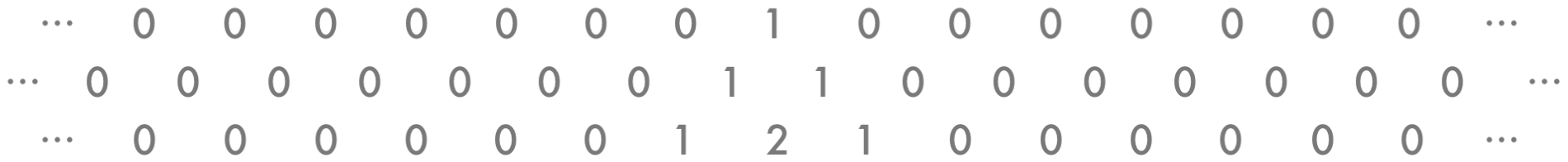
Looking better. Now the rule again to the newest row:

At this point, all those zeroes are getting in the way. So let’s make them invisible.

There, that’s much easier to see. Remember, we haven’t gotten rid of the zeroes; we’ve just hidden them so we can focus on the interesting part.

Continuing the pattern for a few more rows – with each number in the new row being the sum of the two numbers above it – we get:

If we continue this on to infinity, we get a structure known as Pascal’s Triangle.

This curious construction has some very remarkable properties, as discovered by the French mathematician Blaise Pascal (for whom the triangle is named). Let’s start with the basics…