The Golden Angle
So far we’ve already talked about the Golden Ratio as a length. Now let’s talk about its close cousin the Golden Angle.
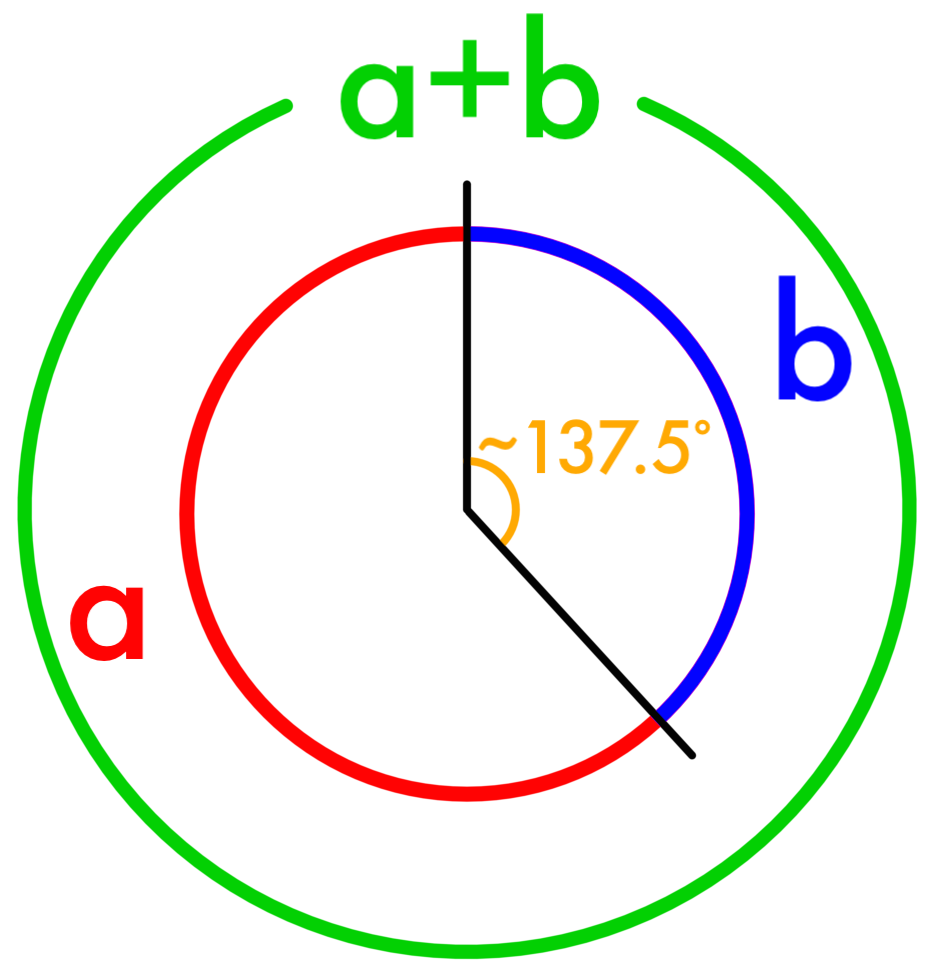
The Golden Angle happens when you break up a circle so that the ratio of the big arc to the little arc is the Golden Ratio. It’s like taking the line definition of the Golden Ratio and wrapping it into a circle – green is to red as red is to blue. The resulting angle (marked in the figure) is the Golden Angle, and if you do the math you find that the angle is about equal to 137.5 degrees.
The Golden Angle is very important if you are a plant. See, if you’re a plant, you have leaves spread all around your stem and you want them to soak up as much sun as possible. So when you sprout a new leaf, you don’t want it to block your other leaves. You want to set it apart by some angle.
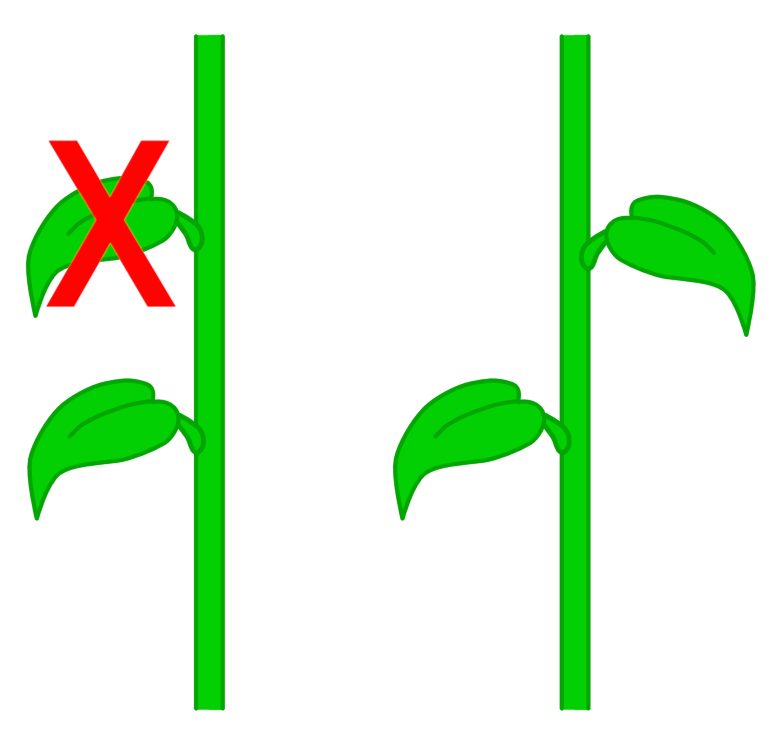
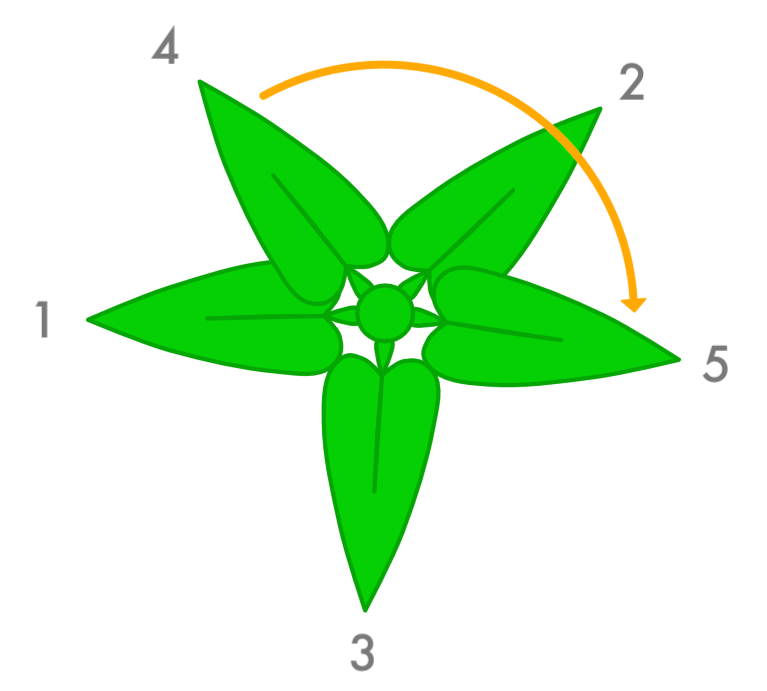
But you’re a plant, so you don’t have a brain, so you want to make it easy on yourself by using the same angle every time you sprout a new leaf. As it turns out, the best way to minimize the overlap of your leaves is to use the Golden Angle. Here’s how it works. Imagine we’re looking at the plant stem from above. We start with one leaf:

Then we rotate by the Golden Angle and sprout another leaf:

Then from there we again rotate by the Golden Angle and sprout a leaf:
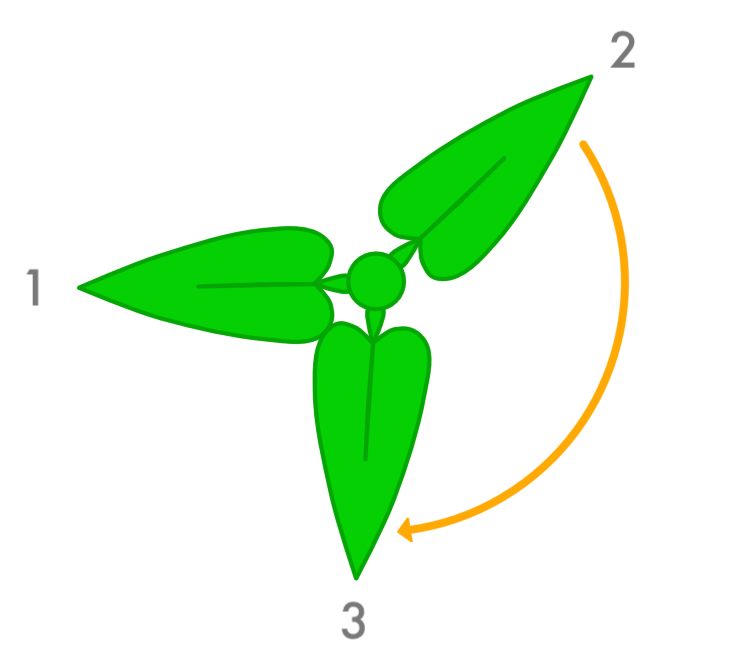
When we rotate again we pass up the first leaf and land in the empty space between it and the second leaf:
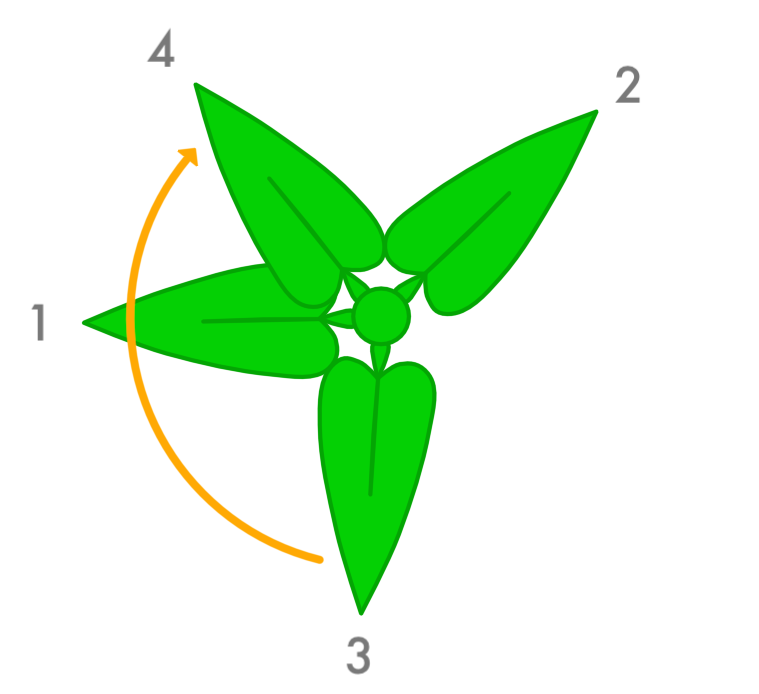
Then the next leaf lands in between the second and third leaves:
And if we keep this up for a while:
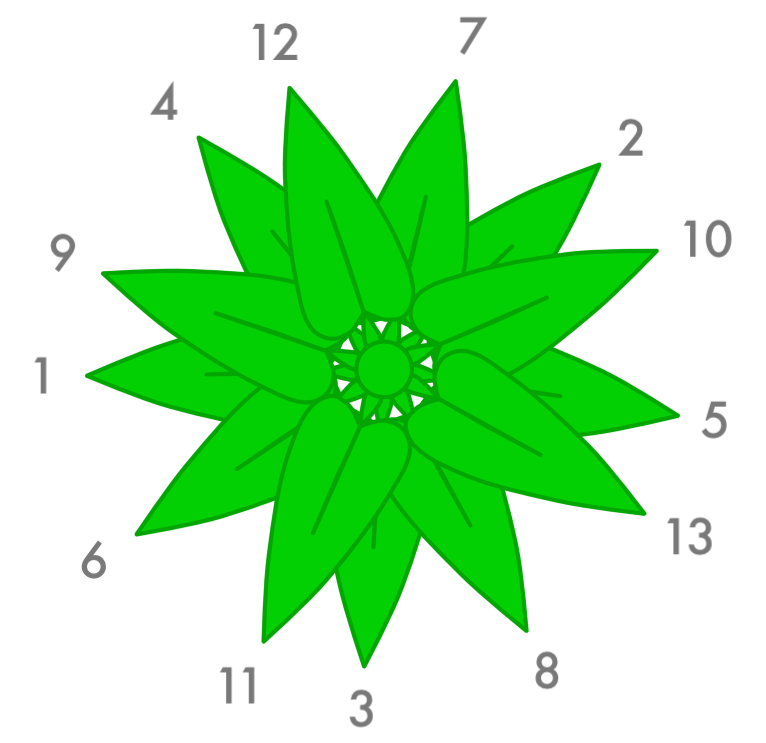
No matter how many leaves you sprout, you’ll always be taking advantage of the spaces in between the previous leaves. You’ll always minimize the overlap! Because the Golden Angle is so convenient this way, you will find the Golden Angle on a lot of plants.
Plants don’t just use the Golden Angle for leaf arrangements. You’ll also find it in the arrangement of sunflower seeds and the centers of other compound flowers.

Each seed in a sunflower is created in the very center of the flower and then migrates outward. In order for the seeds to fill all the space around the center, each seed has to migrate outward in a different direction than the last one did. The angle that determines each new seed’s direction is – you guessed it – the Golden Angle.
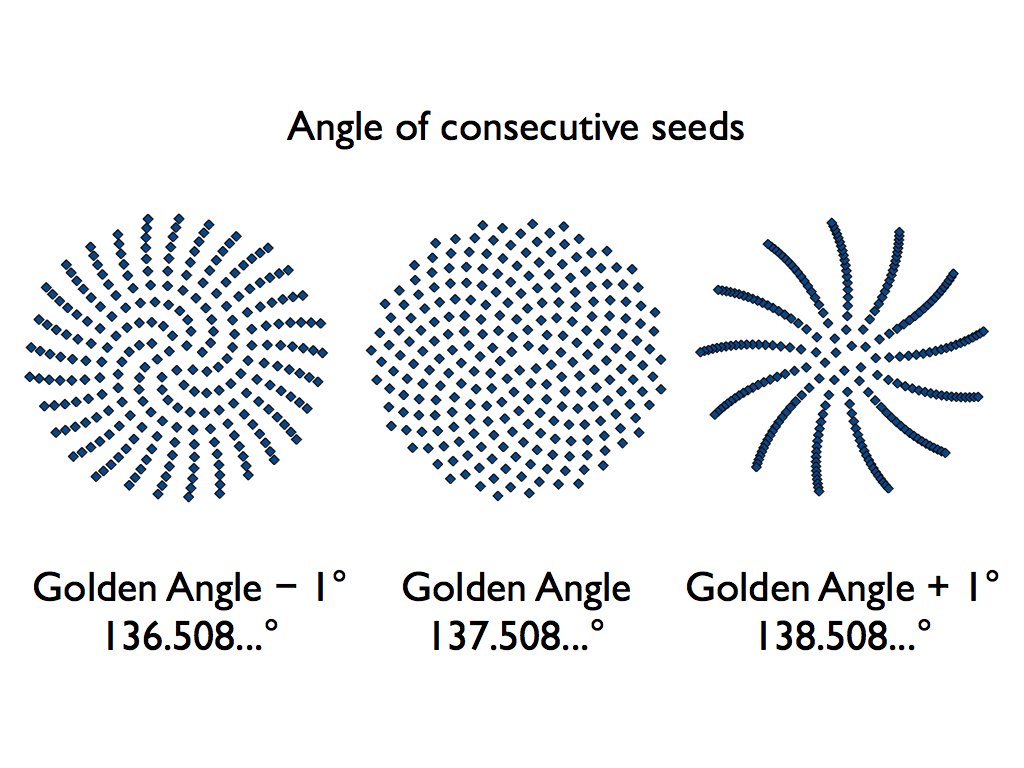
The interlocking spiral pattern looks familiar, doesn’t it? If you’ve read the page on Fibonacci in nature, you’ll remember that when we counted the number of spirals in sunflowers and pinecones, we got Fibonacci numbers. Now we know where the spiral pattern comes from in the first place! The Golden Angle helps explain the recurrence of Fibonacci numbers in nature!
