A Recurrence Riddle - Solution

Let’s start by computing the first few terms of the sequence:

$$ \begin{align} a_1 &= 1 \\ a_2 &= 1 + 2(2) - 1 = 4 \\ a_3 &= 4 + 2(3) - 1 = 9 \\ a_4 &= 9 + 2(4) - 1 = 16 \\ a_5 &= 16 + 2(5) - 1 = 25 \\ a_6 &= 25 + 2(6) - 1 = 36 \end{align} $$

Hmm… that’s interesting…

$$ \begin{align} a_1 &= 1^2 \\ a_2 &= 4 = 2^2 \\ a_3 &= 9 = 3^2 \\ a_4 &= 16 = 4^2 \\ a_5 &= 25 = 5^2 \\ a_6 &= 36 = 6^2 \end{align} $$

Wow – those look like the perfect squares! Let’s take a guess (“conjecture”) that $a_n = n^2$. If we’re right, then $a_{10000}$ will actually be pretty easy to compute.

But taking a guess is only the first step. Now we need to convince ourselves the pattern actually continues all the way out to 10000.

We’ll do this in two different ways. First, here’s a picture proof that adding up the odd numbers (those $2n-1$ terms in Sarah’s puzzle) gives you the perfect squares:

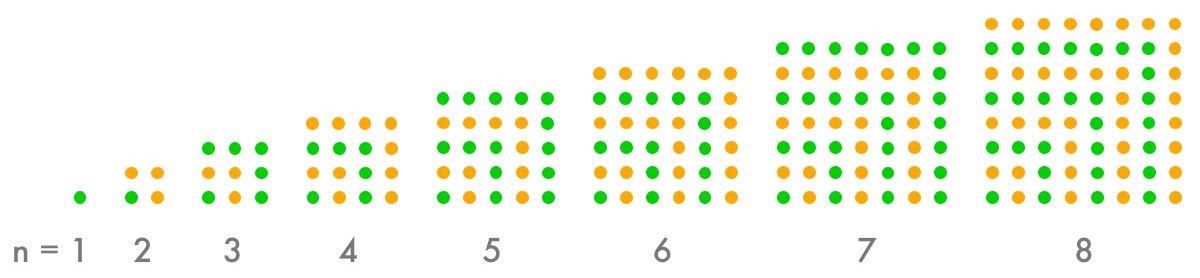
Neat, eh?

In case you’re still not convinced, we’ll prove the pattern using a technique called induction. It works like a line of dominoes: you knock over the first one, and then you show that any domino that falls will knock over the next one in the line. Here we go:

Step 1: the first domino falls down. We already did this while exploring: $a_1 = 1 = 1^2$.

Step 2: any domino that falls will knock down the next one. This is the interesting part. We first assume that some domino falls: $a_k = k^2$ for some $k \ge 1$. Then we look at what happens to the next domino: $a_{k+1} = a_k + 2(k+1) - 1 = a_k + 2k + 1 = k^2 + 2k + 1 = (k+1)^2$. Yay! The next domino has to fall over!

Step 3: because the first domino falls down, and any domino that falls down will knock over the next domino, we conclude that all the dominoes fall down. In math: since $a_1 = 1^2$, and $a_k = k^2$ implies $a_{k+1} = (k+1)^2$, we conclude that $a_n = n^2$ for all $n$.

Hooray! The pattern works! To get $a_{10000}$, then, we just compute:

$$ a_{10000} = 10000^2 = 100000000 $$

And that’s the answer that Amy can give Sarah to get Sarah to put down her book!