Koch Snowflake
The Koch Snowflake is a fractal based on a very simple rule.
The Rule: Whenever you see a straight line, like the one on the left, divide it in thirds and build an equilateral triangle (one with all three sides equal) on the middle third, and erase the base of the equilateral triangle, so that it looks like the thing on the right.
The Koch Snowflake happens when we repeat this process indefinitely on an equilateral triangle. (You could try this on other shapes, too, but I’ll leave those variations for you to explore.) Let’s walk through the steps.
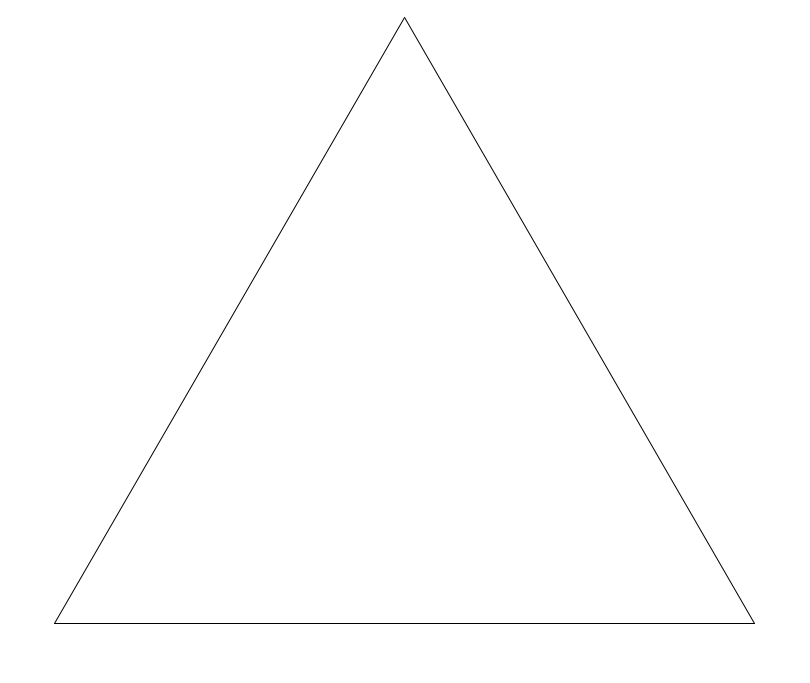
We start with this triangle. Now for each of the three sides, we apply The Rule, so it becomes a 6-pointed star. (The new lines that we just added are in red.)
Then for each side of the 6-pointed star, we apply The Rule again, so it looks like this.
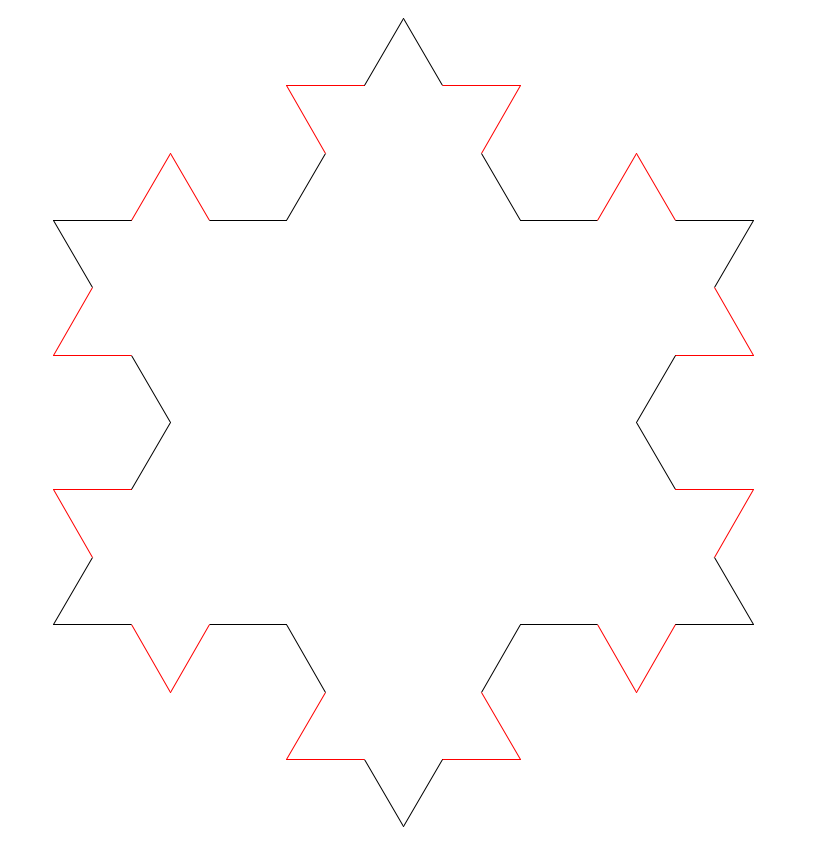
After we apply The Rule again to the result it starts to look much more like a snowflake.
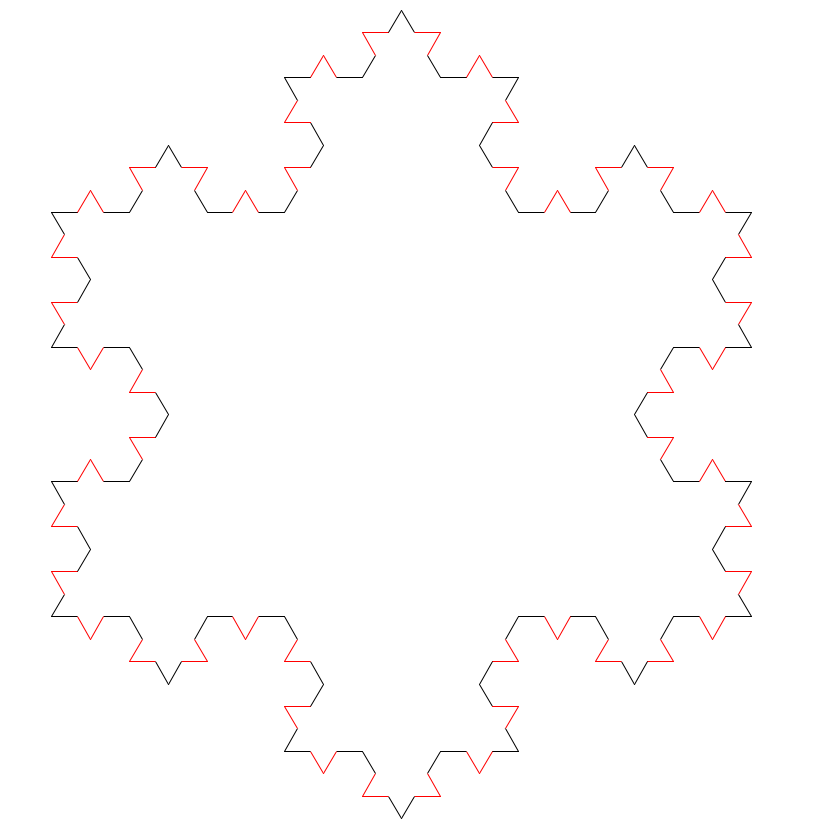
And we can keep going – here’s the next iteration. (I’ll drop the red coloring now that you get the idea.)
And if we continue this on to infinity, we get the Koch Snowflake.
Well, this is a very pretty thing. It looks like the most intricate snowflake that ever fell out of the sky.
Here’s an interesting question: What is the perimeter of the Koch Snowflake? In other words, if you were a bug and you wanted to walk along all those squiggles, how far would you have to travel?
To answer that, let’s look back at our Rule for a moment.
Every time we apply The Rule to a line segment, we’re replacing that segment with $4$ little segments each $\frac{1}{3}$ the length of the original. That means we’re multiplying the length of the segment by $\frac{4}{3}$. If we do this for all the line segments in the snowflake, the net effect is to multiply the entire perimeter by $\frac{4}{3}$. Intuitively, we can see that the perimeter is going to become infinitely squiggly, and that a bug walking along it would need to travel an infinite distance. (That would literally take forever!) If we want to prove it, we can walk through the following logic:
- Our original triangle had some side length, which we can call $s$.
- Since all three sides were the same length, the triangle’s perimeter was $3 \cdot s$.
- When we applied The Rule once, we replaced each line segment with $4$ little segments each $\frac{1}{3}$ the original length, which means we multiplied the length of each segment by $\frac{4}{3}$.
- That made the snowflake’s perimeter $3 \cdot s \cdot \frac{4}{3}$.
- When we applied The Rule a second time, we again multiplied the perimeter by $\frac{4}{3}$.
- That made the snowflake’s perimeter $3 \cdot s \cdot \frac{4}{3} \cdot \frac{4}{3}$ , which equals $3 \cdot s \cdot \left(\frac{4}{3}\right)^2$.
- When we applied The Rule a third time, we again multiplied the perimeter by $\frac{4}{3}$.
- That made the snowflake’s perimeter $3 \cdot s \cdot \left(\frac{4}{3}\right)^3$.
- In general, if we apply The Rule $n$ times, the snowflake’s perimeter will be $3 \cdot s \cdot \left(\frac{4}{3}\right)^n$.
- Since $\frac{4}{3}$ is bigger than 1, as $n$ gets bigger and bigger off to infinity, $\left(\frac{4}{3}\right)^n$ gets bigger and bigger off to infinity as well, which means the perimeter of the snowflake really is infinite.
So the perimeter of the Koch Snowflake is infinite. This fact is really mind-boggling when you consider that the Koch Snowflake has a finite area. You could build a fence around it like the picture below:
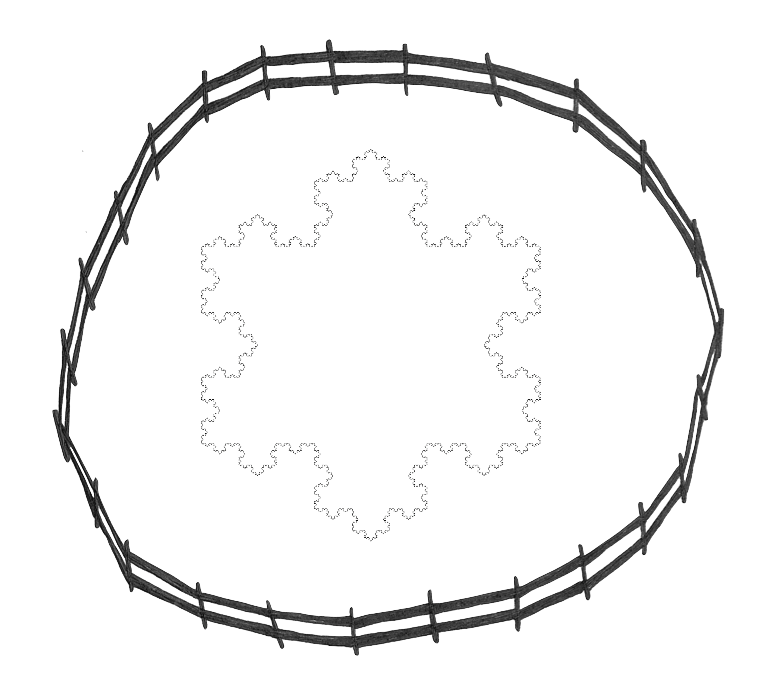
But you could never build a fence that traces its perimeter exactly.
If we’re very careful and clever about it, we can actually calculate the area of the Koch Snowflake. (If you’re curious, the derivation is here.) It turns out that if we start with a triangle with side length $s$, the area of the snowflake is
$$ \dfrac{2s^2\sqrt{3}}{5} $$
The important part, though, is the idea of infinite squiggles all crumpled up in a finite space: infinite perimeter, finite area. This infinite detail is characteristic of fractals; it’s fascinating and mind-blowing. If you’d like to explore more fractals, there are more listed here!