Stargazing - Solution

At first glance, we might think of the star as consisting of many pieces that add together to form the overall shape. But there are a lot of pieces to handle if we think about it this way!

Let’s instead look at the area that’s not covered by the star:

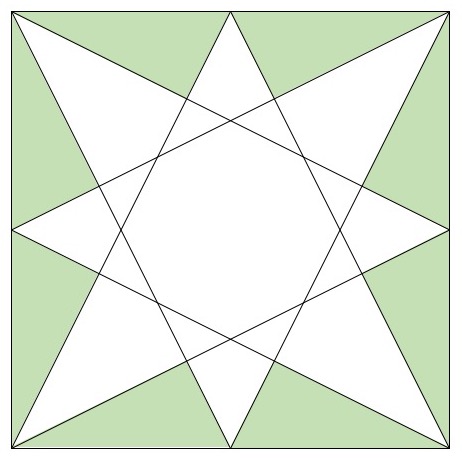
That looks a lot simpler! Because of the star’s symmetry, all of the green triangles are congruent– they have the same shape and the same size. Also, each edge of the star is also an edge of one of the green triangles. So if we can find the edge lengths and area of just one green triangle, we can use that information to compute the perimeter and area of the star.

Now how do we get the dimensions of a green triangle? Let’s draw some more lines! It might be hard to believe this will help us, since there are so many lines already… but we can be very deliberate about which lines we want to see.

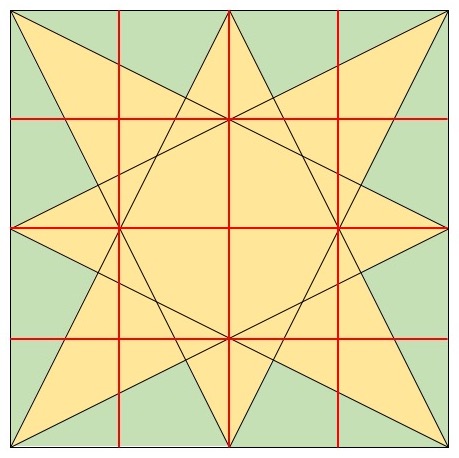
Aha – now we can see a new triangle that might help us with the green one inside it:

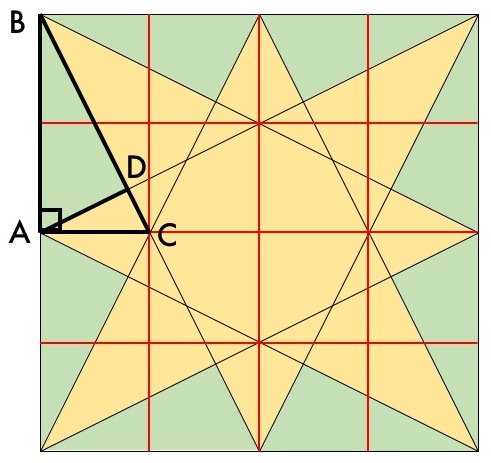
Triangle $BAC$ looks like a useful stepping stone because it’s a right triangle and it lines up nicely with some landmarks we can analyze. For one thing, those new red lines look like they divide the edges of the square into quarters. Do they really? Let’s see:

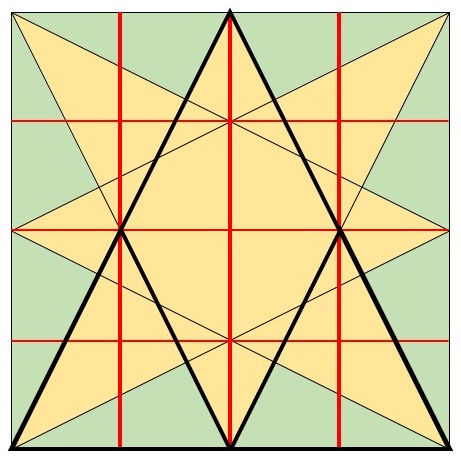
Aha! The symmetry of the problem forces this to be true. (Try drawing a similar diagram for the horizontal lines to check your understanding.) So we now know that in our triangle $BAC$, the length $AB$ is twice the length $AC$, and $AB$ itself is half the side length of the big square.

Now take a look at the angle $ADB$. That sure looks like a right angle, doesn’t it? Let’s try to give a satisfying reason for this rather than just eyeballing it. Here’s one:

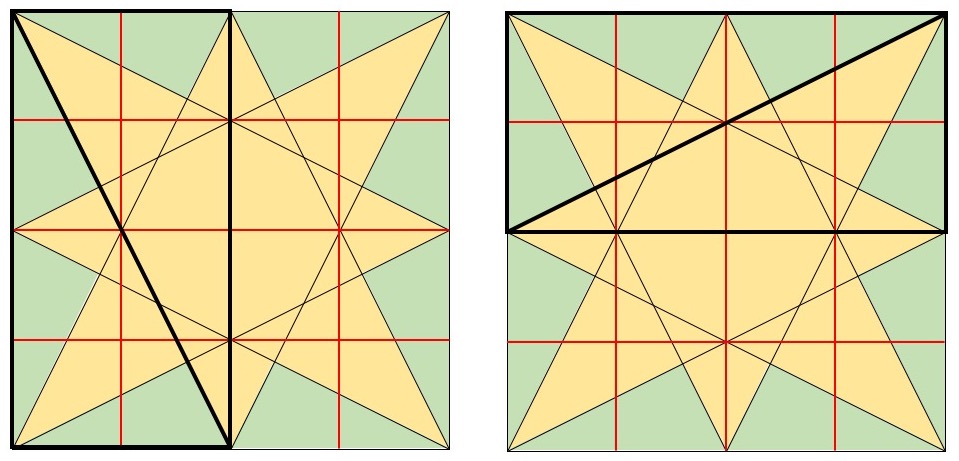
When the bolded rectangle is rotated 90 degrees, its diagonal is rotated 90 degrees also. But segment $BD$ is part of the first diagonal and segment $AD$ is part of the second diagonal. So angle $ADB$ is a right angle after all.

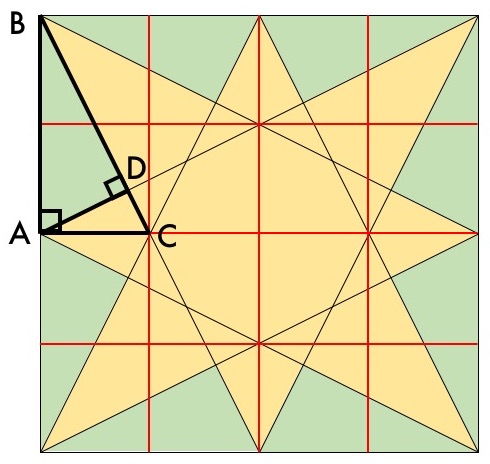
Now we have everything we need to analyze the green triangle! Let’s zoom in on triangle $BAC$:

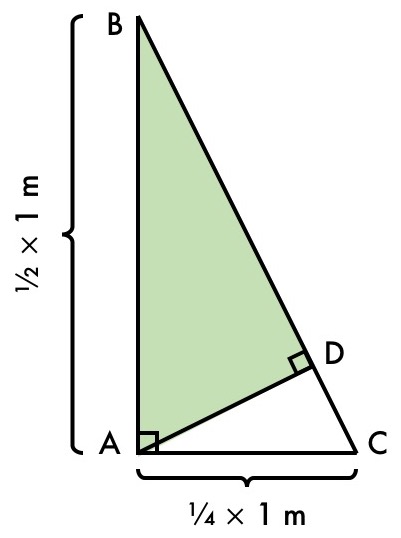
There’s a very important thing to notice here: triangles $BAC$ and $BDA$ are both right triangles that also share an acute angle. That means they’re similar triangles– they have the same shape but not necessarily the same size. So the ratio of their side lengths is the same:

$$\frac{AB}{BC} = \frac{DB}{BA}$$

We know that $AB = BA = \frac{1}{2} \times 100 cm = 50 cm$. We can also find $BC$ using the Pythagorean Theorem:

$$BC^2 = AB^2 + AC^2 = (25 \times 2 cm)^2 + (25 cm)^2 = (25^2 cm^2) \times 5$$

$$BC = 25\sqrt{5} cm$$

That means we can solve for $DB$:

$$DB = \frac{50^2 cm^2}{25\sqrt{5} cm} = \frac{100}{\sqrt{5}} cm = 20\sqrt{5} cm$$

And now that we have $DB$ and $BA$, we can solve for $DA$ also, either using the ratio technique above or using the Pythagorean Theorem. Let’s use the ratio technique again, since it’s cleaner here:

$$\frac{AC}{AB} = \frac{DA}{DB}$$

$$DA = \frac{AC \times DB}{AB} = \frac{25 cm \times 20 \sqrt{5} cm}{50 cm} = 10\sqrt{5} cm$$

We’re almost there! Now we can compute the area of the green triangle $ABD$ as $\frac{1}{2} \times 10\sqrt{5} \times 20\sqrt{5} cm^2 = 500 cm^2$. So the area of the gold star is $10000 cm^2 - 8 \times 500 cm^2 = 6000 cm^2$. The perimeter of the gold star is $8 \times DA + 8 \times DB = (8 \times 10\sqrt{5} + 8 \times 20\sqrt{5}) cm = 240\sqrt{5} cm$. And the final price from Mort’s Tiling is

$$\frac{$0.50}{cm^2} \times 6000 cm^2 + \frac{$0.25}{cm} \times 240\sqrt{5} cm \approx $3134.16$$

Hmm, kind of an expensive decision… Paula might want to get a quote from another contractor to see if she can find a better price.

(If you’re looking for an extra challenge, try finding the area of the octagonal region in the middle of the star!)